

- #RECURSIVE DEFINITION CALCULATOR HOW TO#
- #RECURSIVE DEFINITION CALCULATOR CODE#
- #RECURSIVE DEFINITION CALCULATOR SERIES#
#RECURSIVE DEFINITION CALCULATOR SERIES#
They are particularly useful as a basis for series (essentially describe an operation of adding infinite quantities to a starting quantity), which are generally used in differential equations and the area of mathematics referred to as analysis. Sequences are used to study functions, spaces, and other mathematical structures. A series is convergent if the sequence converges to some limit, while a sequence that does not converge is divergent. Sequences have many applications in various mathematical disciplines due to their properties of convergence. There are many different types of number sequences, three of the most common of which include arithmetic sequences, geometric sequences, and Fibonacci sequences.
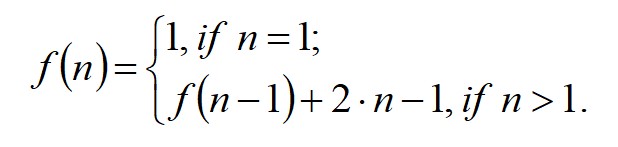
In a number sequence, the order of the sequence is important, and depending on the sequence, it is possible for the same terms to appear multiple times. The individual elements in a sequence is often referred to as term, and the number of terms in a sequence is called its length, which can be infinite. Accordingly, a number sequence is an ordered list of numbers that follow a particular pattern. In mathematics, a sequence is an ordered list of objects. If your input is 4, it will add 1+2+3+4 to output 10 if your input is 5, it will output 15 (meaning 1+2+3+4+5).Example: 1, 3, 5, 7, 9 11, 13. To perfectly grasp the concept of "as a function of input size," imagine you have an algorithm that computes the sum of numbers based on your input. Why is time complexity a function of its input size?
#RECURSIVE DEFINITION CALCULATOR HOW TO#
This will be an in-depth cheatsheet to help you understand how to calculate the time complexity for any algorithm. We will be focusing on time complexity in this guide. Similarly, an algorithm's space complexity specifies the total amount of space or memory required to execute an algorithm as a function of the size of the input. Instead, the time and space complexity as a function of the input's size are what matters.Īn algorithm's time complexity specifies how long it will take to execute an algorithm as a function of its input size. One major underlying factor affecting your program's performance and efficiency is the hardware, OS, and CPU you use.īut you don't consider this when you analyze an algorithm's performance. But it does not tell you how fast your algorithm's runtime is.īig O notation measures the efficiency and performance of your algorithm using time and space complexity. It uses algebraic terms to describe the complexity of an algorithm.īig O defines the runtime required to execute an algorithm by identifying how the performance of your algorithm will change as the input size grows. What is Big O?īig O, also known as Big O notation, represents an algorithm's worst-case complexity.
#RECURSIVE DEFINITION CALCULATOR CODE#
It allows you to estimate how long your code will run on different sets of inputs and measure how effectively your code scales as the size of your input increases. Big O Notation is a metric for determining the efficiency of an algorithm. This is where Big O Notation enters the picture. This is critical for programmers to ensure that their applications run properly and to help them write clean code.

This means that the method you use to arrive at the same solution may differ from mine, but we should both get the same result.īecause there are various ways to solve a problem, there must be a way to evaluate these solutions or algorithms in terms of performance and efficiency (the time it will take for your algorithm to run/execute and the total amount of memory it will consume). You can solve these problems in various ways. An algorithm is a set of well-defined instructions for solving a specific problem.


 0 kommentar(er)
0 kommentar(er)
